on
The Perplexity Trap: Why Standard Metrics Fail for LLM Layer Pruning
Part 1 of 2: An empirical investigation showing that perplexity-based importance metrics provide no predictive signal for reasoning task performance
The Redundancy Assumption
A key assumption that drives a lot of the recent work on LLM compression is that layers that transform representations minimally are less important, and can be removed with limited impact on model performance. The idea is intuitive: if a layer’s output is nearly identical to its input, for example, if its Centered Kernel Alignment score [4] approaches 1 or its Block Influence [1] approaches 0, the layer appears to contribute little and can be removed. LaCo [2] uses Cosine Similarity, while Gromov et al. [6] use Angular Distance to identify prunable layers. SliceGPT [3] also targets redundancy but by pruning dimensions within layers.
Based on the papers mentioned above, the assumption seems to be validated. We can use one or multiple of these importance metrics to determine the impact of the layer. Impact on what, though? Perplexity, yes. Models pruned using these metrics maintain reasonable perplexity, and the correlations between metric values and perplexity often reach statistical significance. What about the impact on task-specific capabilities?
Does a layer’s impact on perplexity correlate with its impact on reasoning capability?
Driven by this question, I performed a systematic evaluation of the correlation between layer importance metrics and reasoning task performance. I found that metrics that predict perplexity impact provide zero signal for reasoning task performance. Worse, the layers that perplexity-based methods identify as safest candidates for removal can be catastrophic for downstream capabilities. The assumption that perplexity serves as a general proxy for model capability does not hold.
Experimental Design
Models and Metrics
I evaluated two production-scale models across their full 32-layer depth:
| Model | Parameters | Layers | Architecture |
|---|---|---|---|
| Mistral-7B-v0.1 | 7.24B | 32 | Grouped Query Attention, Sliding Window |
| Llama-3.1-8B | 8.03B | 32 | Standard Transformer, RoPE |
For each model, I computed six importance metrics on 256 calibration samples from WikiText-2:
| Metric | Definition | Pruning Signal |
|---|---|---|
| Block Influence | Relative hidden state change: $\lVert H_i - H_{i-1}\rVert / \lVert H_{i-1}\rVert$ | Low = safe |
| Angular Distance | Angle between representations: $\arccos(\cos(H_{i-1}, H_i))$ | Low = safe |
| CKA | Centered Kernel Alignment: $\frac{\lVert H_{i-1}^T H_i\rVert_F^2}{\lVert H_{i-1}^T H_{i-1}\rVert_F \lVert H_i^T H_i\rVert_F}$ | High = safe |
| MSE | Mean squared difference: $\text{mean}((H_i - H_{i-1})^2)$ | Low = safe |
| L2 Norm | Euclidean distance: $\lVert H_i - H_{i-1}\rVert_2$ | Low = safe |
| Cosine Similarity | Directional similarity: $\cos(H_{i-1}, H_i)$ | High = safe |
Ablation Protocol
For each layer, I performed a complete removal (excising the layer while preserving the residual connection) and measured:
- Perplexity on WikiText-2 (standard language modeling metric)
- GSM8K accuracy [5] (100 samples, 5-shot prompting, mathematical reasoning)
For this study, I focused on GSM8K for mathematical reasoning evaluation. GSM8K consists of grade-school math word problems that require multi-step arithmetic reasoning. Here is an example:
Example GSM8K problem:
Q: Janet’s ducks lay 16 eggs per day. She eats 3 for breakfast and bakes muffins with 4. She sells the rest for$2each. How much does she make daily?
A: 16 - 3 - 4 = 9 eggs sold. 9 x$2=$18. Answer: 18
This produced 64 complete ablations (32 layers x 2 models), with both perplexity and reasoning measurements for every configuration.
The Core Finding: Zero Correlation
The correlation between perplexity impact and GSM8K accuracy impact is effectively zero.
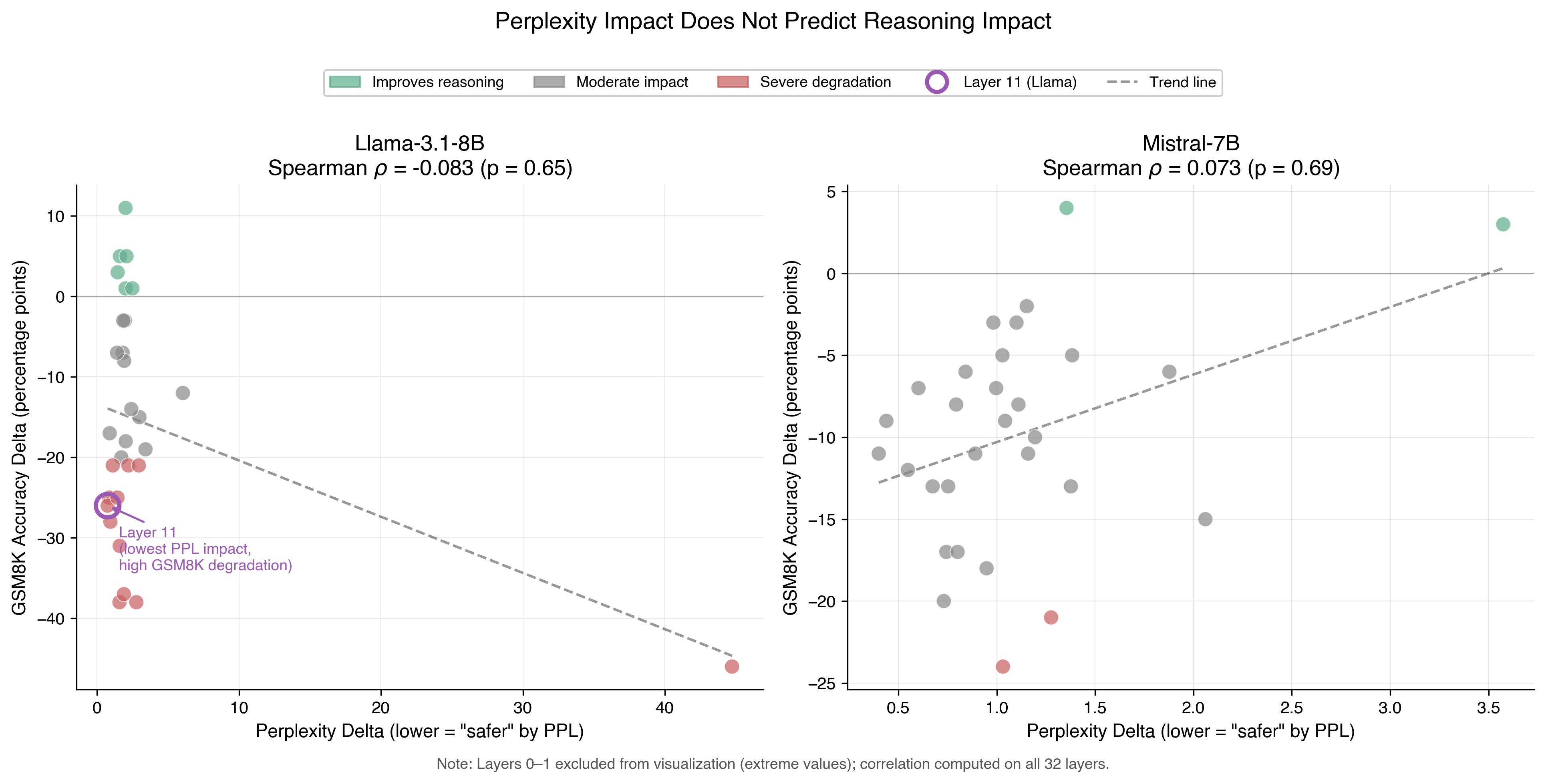Figure 1: Scatter plots showing perplexity delta versus GSM8K accuracy delta for each layer removal. Each point represents one layer; its x-coordinate is the perplexity increase when removed, and its y-coordinate is the change in GSM8K accuracy.
The Spearman correlation is near zero for both models ($\rho = -0.083$ for Llama, $\rho = 0.073$ for Mistral). This is not weak correlation or modest predictive power. It is an absence of relationship. Perplexity-optimal pruning decisions provide no signal for reasoning capability preservation.
The Layer 11 Paradox
Let’s take a closer look at Llama-3.1-8B’s Layer 11:
| Metric | Layer 11 Value | Layer 11 Rank | Interpretation |
|---|---|---|---|
| Perplexity impact | +0.74 | #1 lowest | Top pruning candidate |
| CKA score | 0.9999 | Near-maximum | Appears highly redundant |
| GSM8K impact | -26 points | Among worst | Critical for reasoning |
If one uses a perplexity-based criterion, Layer 11 would be the safest choice for pruning. The intact model’s perplexity on WikiText-2 is 15.31, and removing Layer 11 would put us just 0.74 above that. The CKA score also shows that Layer 11 contributes minimal computation and should be safe to remove. When it is removed, GSM8K accuracy drops from 48% (intact model baseline) to 22%, cutting reasoning performance in half.
The Top Pruning Candidates Are Reasoning-Critical
Layer 11 was just one example to illustrate the disconnect between perplexity and reasoning. I notice that the layers with the lowest perplexity impact are consistently among the most damaging for reasoning:
Table: Llama-3.1-8B Layers Ranked by Perplexity Safety vs. Reasoning Impact
| Layer | PPL Rank | PPL $\Delta$ | GSM8K $\Delta$ | Reasoning Category |
|---|---|---|---|---|
| 11 | #1 | +0.74 | -26% | Catastrophic |
| 10 | #2 | +0.85 | -25% | Severe |
| 8 | #3 | +0.89 | -17% | High |
| 12 | #4 | +0.94 | -28% | Catastrophic |
| 9 | #5 | +1.10 | -21% | Severe |
The layers with lowest perplexity impact all produce double-digit reasoning degradation. Perplexity-guided pruning would select precisely the layers that destroy downstream reasoning capability as also shown in the figure below:
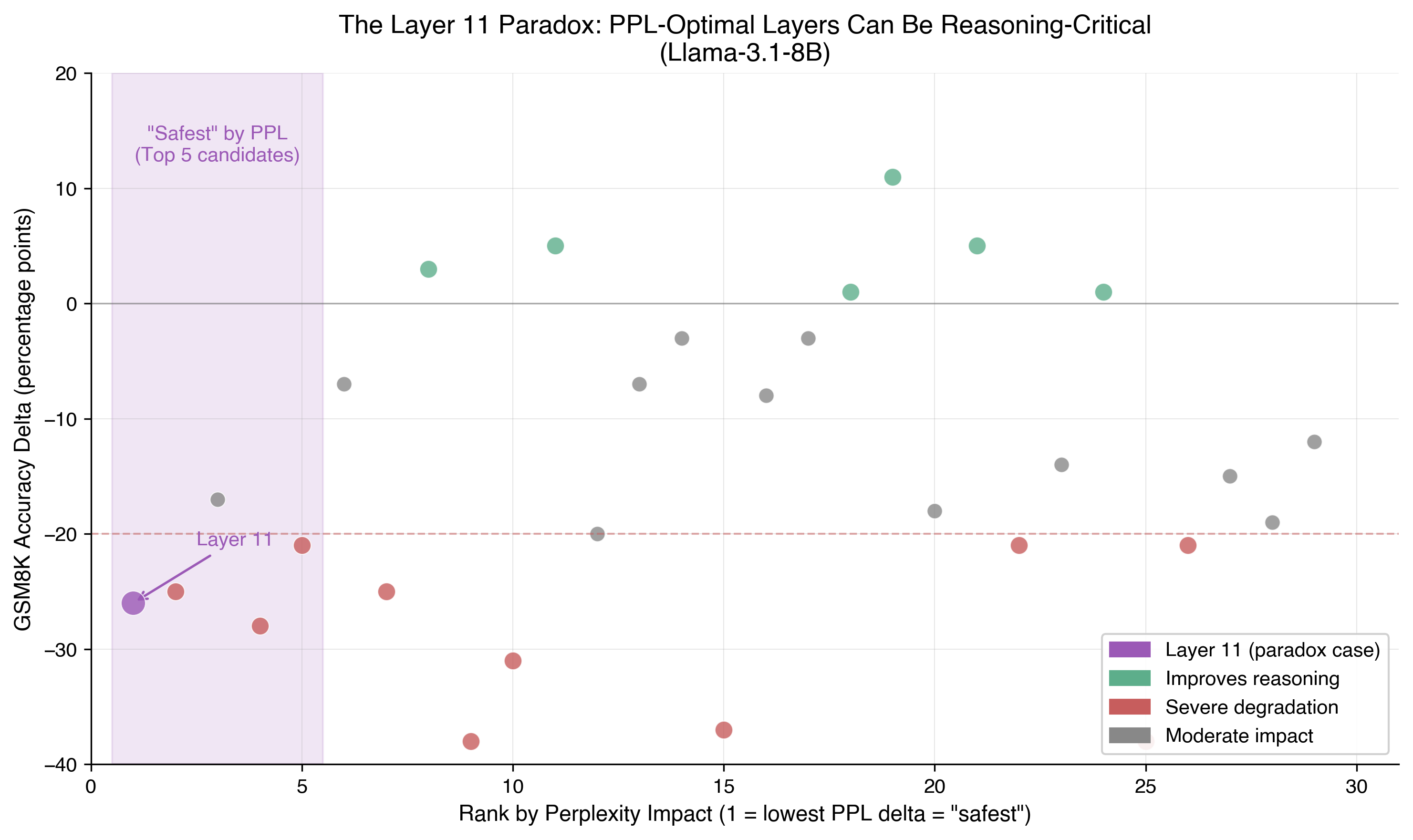Figure 2: Layers ranked by perplexity impact (lower rank = safer to prune by PPL metrics) vs their GSM8K accuracy impact. The shaded region shows the top 5 “safest” layers by perplexity, but all produce substantial reasoning harm.
In Mistral-7B-v0.1 (baseline: 37% GSM8K), the pattern is equally stark: the top 5 layers ranked safest by perplexity (Layers 14, 8, 12, 7, 9 with PPL deltas of +0.40 to +0.67) all cause 7 to 13 percentage point GSM8K degradation. Layer 11, ranked #6 for PPL safety (delta +0.73), causes the most severe reasoning harm at -20 points. The failure mode persists across architectures.
Why Existing Metrics Work for Perplexity
Before addressing why metrics fail for reasoning, it is worth acknowledging where they succeed.
For perplexity prediction, the redundancy assumption shows partial validity:
Table: Metric-Perplexity Correlations (Bonferroni-Corrected, $\alpha = 0.0083$)
| Metric | Mistral $\rho$ | Bonferroni Sig. | Llama $\rho$ | Bonferroni Sig. |
|---|---|---|---|---|
| Block Influence | 0.571 | Yes | 0.396 | No |
| Angular Distance | 0.585 | Yes | 0.348 | No |
| CKA | -0.357 | No | -0.491 | Yes |
| Cosine Similarity | -0.577 | Yes | -0.348 | No |
| MSE | 0.206 | No | 0.202 | No |
| L2 Norm | 0.206 | No | 0.202 | No |
CKA [4] demonstrates the best cross-model reliability for perplexity prediction. If the goal is minimizing perplexity degradation and perplexity alone, these metrics provide useful signal. We just need to be aware that perplexity and reasoning task performance are uncorrelated.
Analysis: Why the Disconnect Exists
Perplexity Measures Token Prediction, Not Reasoning
Perplexity quantifies how well a model predicts the next token in a sequence. It rewards confident predictions on typical linguistic patterns. A layer that smooths representations, interpolating toward common patterns, might reduce perplexity while degrading the precise feature distinctions needed for multi-step reasoning.
Mathematical problem-solving requires maintaining exact numerical values through long chains of computation. A layer that makes “small” transformations, and therefore has high CKA or low Block Influence, might still perform critical operations on specific dimensions encoding intermediate calculation results.
Task-Specific Circuits
Recent mechanistic interpretability work suggests that specific capabilities in LLMs rely on identifiable circuits - sparse networks of attention heads and MLP neurons that implement particular functions. Mathematical reasoning likely depends on circuits that:
- Parse numerical expressions
- Maintain intermediate values
- Execute arithmetic operations
- Track multi-step dependencies
Such circuits may pass through layers that otherwise appear redundant. A layer’s importance for reasoning is determined by whether it participates in reasoning circuits, not by its overall transformation magnitude.
The Quadrant Analysis
The figure below ties the study together, most importantly, highlighting the perplexity trap within the lower left quadrant. These are layers one would pick first to prune (given their low perplexity impact), and may find that they were critical for the downstream task.
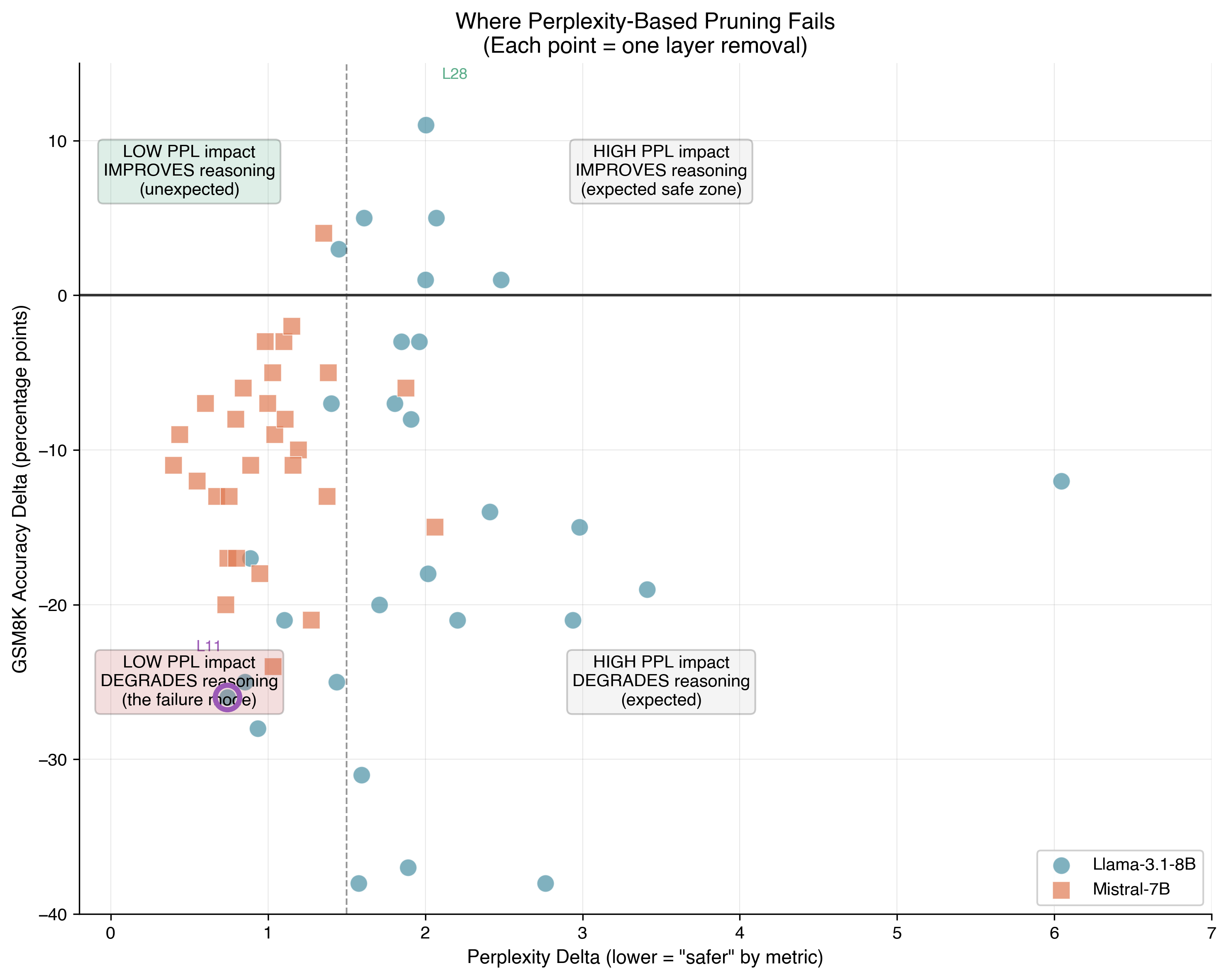Figure 3: Each layer plotted by perplexity impact (x-axis, log scale) vs GSM8K reasoning impact (y-axis). Layer 11 exemplifies the perplexity trap: minimal PPL impact, severe reasoning harm.
Statistical Considerations
The GSM8K evaluations used 100 samples per configuration, yielding standard errors of approximately 5 percentage points. Individual layer comparisons have overlapping confidence intervals with baseline. However:
- The zero correlation finding is robust ($p > 0.65$ for both models)
- The pattern of low-PPL / high-reasoning-impact layers appears in both models
- The magnitude of reasoning degradation for “safe” layers is large (-20% to -28%)
Larger sample sizes would strengthen confidence in individual layer rankings but would not change the fundamental finding: perplexity does not predict reasoning impact.
Summary
The assumption that layers with minimal representational transformation can be safely removed does not hold for reasoning tasks. Layer importance is fundamentally task-dependent. The same layer can be redundant for one task and critical for another.
References
[1] Men, X., et al. (2024). ShortGPT: Layers in Large Language Models are More Redundant Than You Expect. arXiv:2403.03853.
[2] Yang, M., et al. (2024). LaCo: Large Language Model Pruning via Layer Collapse. arXiv:2402.11187.
[3] Ashkboos, S., et al. (2024). SliceGPT: Compress Large Language Models by Deleting Rows and Columns. arXiv:2401.15024.
[4] Kornblith, S., et al. (2019). Similarity of Neural Network Representations Revisited. ICML 2019.
[5] Cobbe, K., et al. (2021). Training Verifiers to Solve Math Word Problems. arXiv:2110.14168.
[6] Gromov, A., et al. (2024). The Unreasonable Ineffectiveness of the Deeper Layers. arXiv:2403.17887.
January 2026. Experiments conducted on NVIDIA L40S GPUs.