on
When Less is More: Layer Removal That Improves LLM Reasoning
Part 2 of 2: Systematic analysis shows that removing specific layers improves mathematical reasoning performance by up to 11 percentage points
The Core Finding
In The Perplexity Trap, I documented which layers harm reasoning when removed. The natural follow-up question:
Are there layers whose removal benefits reasoning?
My systematic ablation reveals that there are. Removing Layer 28 from Llama-3.1-8B improves GSM8K accuracy from 48% to 59%, an 11 percentage point improvement from eliminating computation.
This finding is a direct consequence of the perplexity-reasoning disconnect. If a layer’s contribution to perplexity tells us nothing about its contribution to reasoning, then layers optimized for language modeling might actively interfere with precise computation.
Recap: Perplexity Does Not Predict Reasoning
Recall from Part 1 that the correlation between a layer’s perplexity impact and its reasoning impact is effectively zero.
| Model | PPL-GSM8K Correlation | p-value |
|---|---|---|
| Mistral-7B | $\rho = +0.073$ | 0.69 |
| Llama-3.1-8B | $\rho = -0.083$ | 0.65 |
A layer’s perplexity impact tells us nothing about its reasoning impact, and the layers that appear safest by perplexity are often the most harmful for reasoning.
Layer-by-Layer Reasoning Impact
I evaluated GSM8K [5] accuracy for all 32 single-layer ablations in both Llama-3.1-8B and Mistral-7B-v0.1.
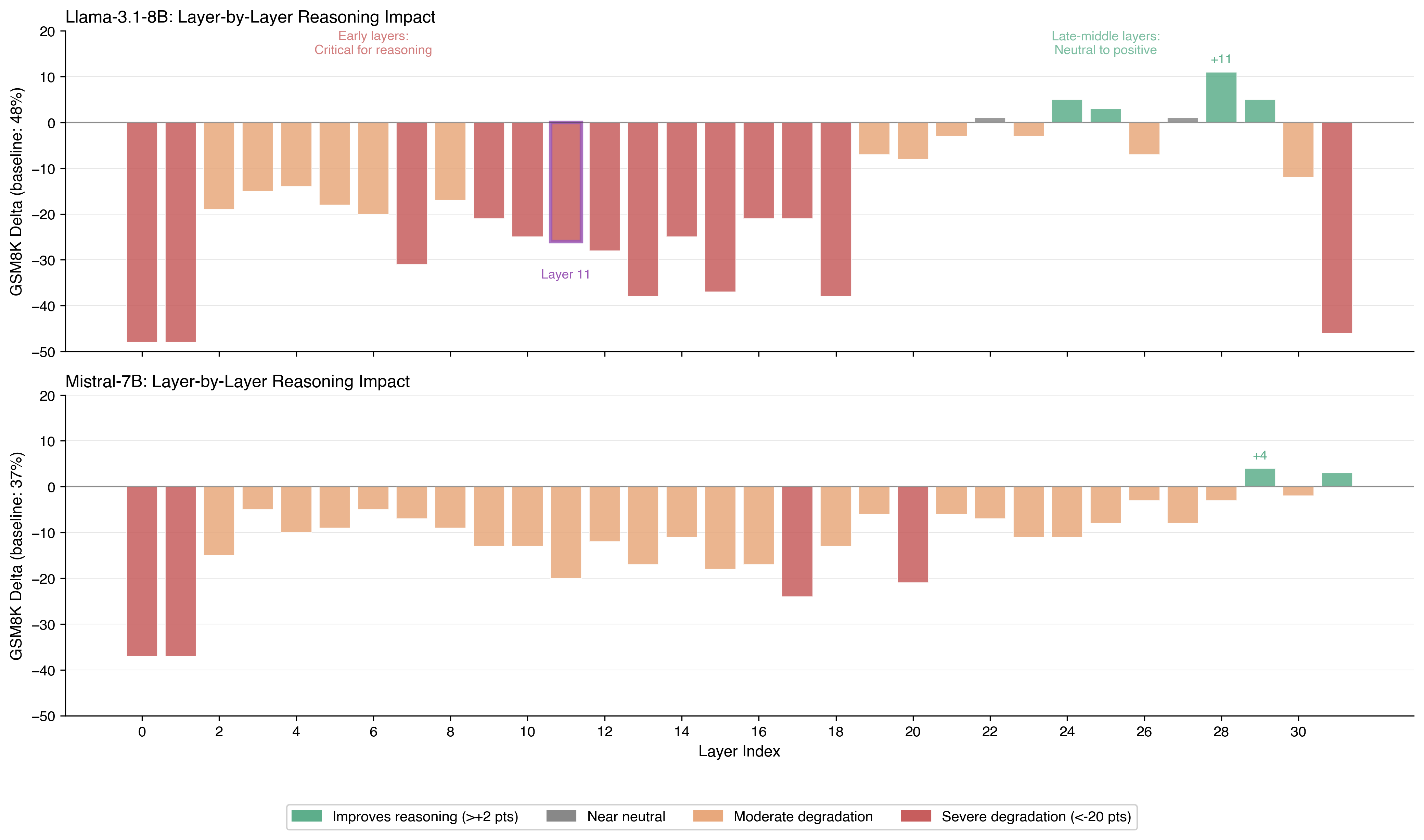 Figure 1: GSM8K accuracy change for each layer removal.
Figure 1: GSM8K accuracy change for each layer removal.
Green bars indicate reasoning improvement (accuracy above baseline); red bars indicate degradation. The pattern shows distinct regions: early layers (0-1) are universally catastrophic, early-middle layers (2-18) cause moderate-to-severe harm, late-middle layers (22-29) show neutral-to-positive effects in Llama, and the final layer (31) is critical. Note the improvement cluster in layers 24-29 for Llama and layer 29 for Mistral.
Llama-3.1-8B: Layers That Improve Reasoning
| Layer Removed | GSM8K Accuracy | Change vs. Baseline | Perplexity $\Delta$ |
|---|---|---|---|
| 28 | 59% | +11 points | +2.00 |
| 24 | 53% | +5 points | +1.61 |
| 29 | 53% | +5 points | +2.07 |
| 25 | 51% | +3 points | +1.45 |
| 22 | 49% | +1 point | +2.00 |
| 27 | 49% | +1 point | +2.48 |
| Baseline | 48% | — | — |
Six layers (22, 24, 25, 27, 28, 29) produce positive effects when removed. Layer 28 alone yields an 11-point improvement.
Mistral-7B-v0.1: Layers That Improve Reasoning
| Layer Removed | GSM8K Accuracy | Change vs. Baseline |
|---|---|---|
| 29 | 41% | +4 points |
| Baseline | 37% | — |
The effect is smaller but present: removing Layer 29 improves accuracy by 4 points.
The U-Shaped Pattern
Examining the full layer-by-layer results reveals a structured pattern. The table below shows Llama-3.1-8B, but Mistral-7B-v0.1 exhibits a similar trend: late layers (roughly the final 25% of the network) show neutral-to-positive effects when removed, while early and middle layers are critical.
Table: Llama-3.1-8B GSM8K Impact by Layer Region
| Layer Range | Typical GSM8K Impact | Interpretation |
|---|---|---|
| 0-1 | -48% (catastrophic) | Foundational layers |
| 2-6 | -14% to -20% | Early processing, significant harm |
| 7 | -31% | Critical layer |
| 8-18 | -17% to -38% (variable) | Core processing, mostly critical |
| 19-21 | -3% to -8% | Transitional, moderate harm |
| 22-29 | -7% to +11% | Interference zone |
| 30 | -12% | Late processing |
| 31 | -46% | Output preparation, critical |
The pattern forms a rough U-shape when plotting impact against layer index:
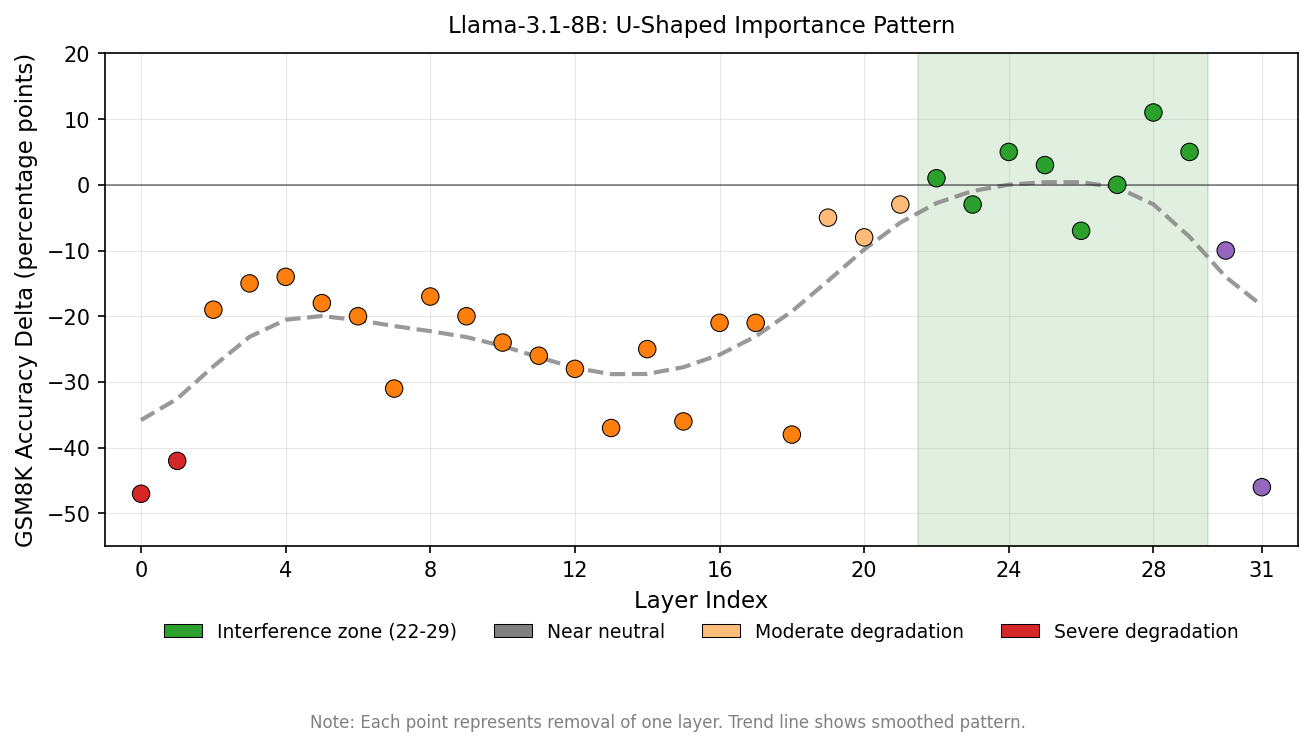 Figure 2: GSM8K accuracy change for each layer removal in Llama-3.1-8B. The U-shape shows early layers are catastrophic, middle layers are critical, and late layers (22-29) form an “interference zone” where removal is neutral or beneficial.
Figure 2: GSM8K accuracy change for each layer removal in Llama-3.1-8B. The U-shape shows early layers are catastrophic, middle layers are critical, and late layers (22-29) form an “interference zone” where removal is neutral or beneficial.
The “interference zone” in layers 22-29 is where removal improves or maintains reasoning performance. These layers add computation that provides no benefit and may actively harm mathematical reasoning.
Hypothesis: Task-Specific Interference
Why would removing layers improve performance? One hypothesis consistent with these results:
Certain layers perform transformations that benefit general language modeling (reducing perplexity) while degrading specific capabilities (mathematical reasoning).
The Interference Mechanism
Late-middle layers (22-29 in Llama) may perform operations that:
-
Smooth representations: Interpolating toward common patterns, which helps predict typical text but blurs distinctions critical for mathematical computation
-
Introduce task-irrelevant features: Adding information relevant to general language understanding that interferes with the sparse circuits used for arithmetic
-
Overwrite intermediate values: Mathematical reasoning requires maintaining precise intermediate results through computation chains; certain layers may corrupt these values
-
Add uncertainty: Calibrating confidence in ways appropriate for text generation but harmful for problems with definite answers
Evidence Supporting the Hypothesis
Several observations align with task-specific interference:
Perplexity-Reasoning Anticorrelation in Interference Zone
For layers 22-29 specifically:
- Removing Layer 28 increases perplexity (+2.00) but improves GSM8K (+11%)
- Removing Layer 25 increases perplexity (+1.45) but improves GSM8K (+3%)
The layers that most benefit reasoning are not perplexity-neutral; in fact, they actively increase perplexity when removed. This suggests they perform real computation, but computation that happens to be counterproductive for reasoning.
Late-Layer Positioning
The interference zone occurs in the final third of the network. This positioning is consistent with layers that perform high-level refinement: smoothing outputs, calibrating confidence, interpolating toward common patterns. Such operations might help with fluent text generation while harming precise computation.
Cross-Model Consistency
Both Mistral-7B and Llama-3.1-8B show improvement from removing late layers, despite different architectures (Grouped Query Attention vs. standard attention, Sliding Window vs. full attention). The specific layers differ, but the general pattern holds: late layers can interfere with reasoning.
Notably, Gromov et al. [6] find that late layers contribute less to perplexity than expected. My results extend and complicate their findings: these layers are indeed less effective for perplexity, but for reasoning tasks, removing them does not merely maintain performance, it improves it. The ineffectiveness they observed may actually be active interference when the task demands precise computation.
Statistical Considerations
The improvements observed require careful statistical interpretation. Each GSM8K [5] evaluation used 100 samples. With binary outcomes (correct/incorrect), the standard error is approximately:
\[SE = \sqrt{\frac{p(1-p)}{n}} \approx 0.05 \text{ (for } p \approx 0.5 \text{, } n = 100 \text{)}\]For the 11-point improvement (Layer 28: 59% vs. Baseline: 48%):
- Standard error of difference: $\approx 7\%$
- 95% CI for difference: approximately $[-3\%, +25\%]$
The confidence interval includes zero. A single 11-point improvement, in isolation, would not reach conventional significance thresholds. However, the clustering of improving layers in the 22-29 region and cross-model consistency suggest a real pattern rather than noise.
Complete Results
Llama-3.1-8B: All 32 Layers
Baseline: 48% GSM8K accuracy, 15.31 perplexity
| Layer | GSM8K | $\Delta$ | PPL $\Delta$ | Layer | GSM8K | $\Delta$ | PPL $\Delta$ | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0% | -48 | +10183 | 16 | 27% | -21 | +2.20 | |
| 1 | 0% | -48 | +19103 | 17 | 27% | -21 | +2.94 | |
| 2 | 29% | -19 | +3.41 | 18 | 10% | -38 | +2.76 | |
| 3 | 33% | -15 | +2.98 | 19 | 41% | -7 | +1.80 | |
| 4 | 34% | -14 | +2.41 | 20 | 40% | -8 | +1.91 | |
| 5 | 30% | -18 | +2.02 | 21 | 45% | -3 | +1.96 | |
| 6 | 28% | -20 | +1.71 | 22 | 49% | +1 | +2.00 | |
| 7 | 17% | -31 | +1.59 | 23 | 45% | -3 | +1.85 | |
| 8 | 31% | -17 | +0.89 | 24 | 53% | +5 | +1.61 | |
| 9 | 27% | -21 | +1.10 | 25 | 51% | +3 | +1.45 | |
| 10 | 23% | -25 | +0.85 | 26 | 41% | -7 | +1.40 | |
| 11 | 22% | -26 | +0.74 | 27 | 49% | +1 | +2.48 | |
| 12 | 20% | -28 | +0.94 | 28 | 59% | +11 | +2.00 | |
| 13 | 10% | -38 | +1.58 | 29 | 53% | +5 | +2.07 | |
| 14 | 23% | -25 | +1.44 | 30 | 36% | -12 | +6.04 | |
| 15 | 11% | -37 | +1.89 | 31 | 2% | -46 | +44.73 |
Mistral-7B-v0.1: All 32 Layers
Baseline: 37% GSM8K accuracy, 14.66 perplexity
| Layer | GSM8K | $\Delta$ | Layer | GSM8K | $\Delta$ | |
|---|---|---|---|---|---|---|
| 0 | 0% | -37 | 16 | 20% | -17 | |
| 1 | 0% | -37 | 17 | 13% | -24 | |
| 2 | 22% | -15 | 18 | 24% | -13 | |
| 3 | 32% | -5 | 19 | 31% | -6 | |
| 4 | 27% | -10 | 20 | 16% | -21 | |
| 5 | 28% | -9 | 21 | 31% | -6 | |
| 6 | 32% | -5 | 22 | 30% | -7 | |
| 7 | 30% | -7 | 23 | 26% | -11 | |
| 8 | 28% | -9 | 24 | 26% | -11 | |
| 9 | 24% | -13 | 25 | 29% | -8 | |
| 10 | 24% | -13 | 26 | 34% | -3 | |
| 11 | 17% | -20 | 27 | 29% | -8 | |
| 12 | 25% | -12 | 28 | 34% | -3 | |
| 13 | 20% | -17 | 29 | 41% | +4 | |
| 14 | 26% | -11 | 30 | 35% | -2 | |
| 15 | 19% | -18 | 31 | 40% | +3 |
Open Questions
This study characterized single-layer removal in two model families. Open questions include:
- Multi-layer interactions: Do improvements compound when removing multiple “interfering” layers together? If Layer 28 removal yields +11% and Layer 29 removal yields +5%, does removing both yield +16%? More? Less?
- Task generalization: Do the same layers interfere with other reasoning tasks (code generation, logical deduction, factual QA)?
- Scale dependence: Do larger or smaller models show the same patterns?
- Architecture dependence: I studied Llama and Mistral. Do results generalize to other architectures (e.g., Mamba, RWKV)?
- Mechanistic analysis: What computations do the interfering layers perform? Activation patching and attention pattern analysis could reveal what these layers contribute to language modeling that harms reasoning.
- Task-specific metrics: Can importance metrics be developed that predict task performance rather than perplexity? Current metrics like CKA and Block Influence are optimized for representational similarity, not task-specific capability.
Conclusion
The systematic evaluation of 64 layer ablations across two models shows that layer importance is fundamentally task-dependent. The central findings:
-
Perplexity and reasoning are uncorrelated: Correlation is effectively zero ($\rho \approx 0$, $p > 0.65$)
-
Selective removal improves reasoning: Layer 28 in Llama-3.1-8B yields +11 percentage points; late layers show improvement in both models
-
A consistent interference zone exists: Layers 22-29 in Llama show neutral-to-positive reasoning effects
-
No universal importance metric exists: What helps one task may hurt another
-
Task-specific evaluation is mandatory: Validate pruning decisions on target tasks, not proxy metrics
Appendix: Experimental Details
Hardware
- NVIDIA L40S (48GB VRAM)
- NVIDIA A100 (80GB VRAM)
- 256GB System RAM
Software
- Python 3.10
- PyTorch 2.1.0
- Transformers 4.36.0
- lm-evaluation-harness 0.4.0
GSM8K Evaluation
- 100 samples per configuration
- 5-shot prompting
- Strict match evaluation (exact numerical answer)
- Reproducible random seed
Layer Ablation
- Layer removal preserves residual connection
- No fine-tuning or adaptation after removal
- Full precision (bf16 for Llama, fp16 for Mistral)
References
[1] Men, X., et al. (2024). ShortGPT: Layers in Large Language Models are More Redundant Than You Expect. arXiv:2403.03853.
[2] Yang, M., et al. (2024). LaCo: Large Language Model Pruning via Layer Collapse. arXiv:2402.11187.
[3] Ashkboos, S., et al. (2024). SliceGPT: Compress Large Language Models by Deleting Rows and Columns. arXiv:2401.15024.
[4] Kornblith, S., et al. (2019). Similarity of Neural Network Representations Revisited. ICML 2019.
[5] Cobbe, K., et al. (2021). Training Verifiers to Solve Math Word Problems. arXiv:2110.14168.
[6] Gromov, A., et al. (2024). The Unreasonable Ineffectiveness of the Deeper Layers. arXiv:2403.17887.
January 2026. Experiments conducted on NVIDIA L40S GPUs.